目录

旋转-θ角度的矩阵 对照旋转θ角度的矩阵是转置 从定义上来看,是逆

旋转的逆等于旋转的转置(正交矩阵)

Viewing观测变换

三维变换

三维旋转 循环对称 向量叉乘

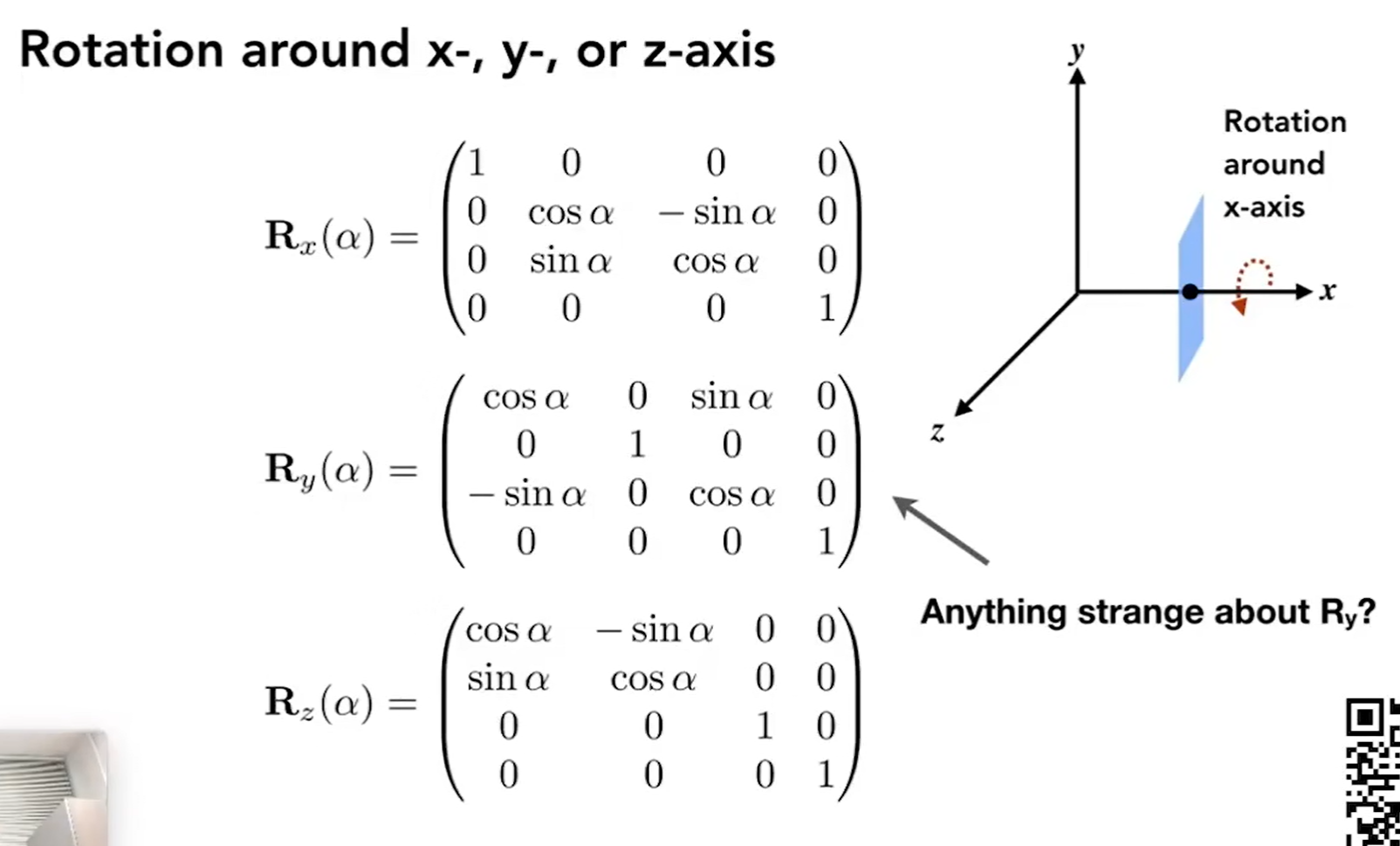
一般性的旋转

旋转公式

给一个选择矩阵,旋转轴和选择角度

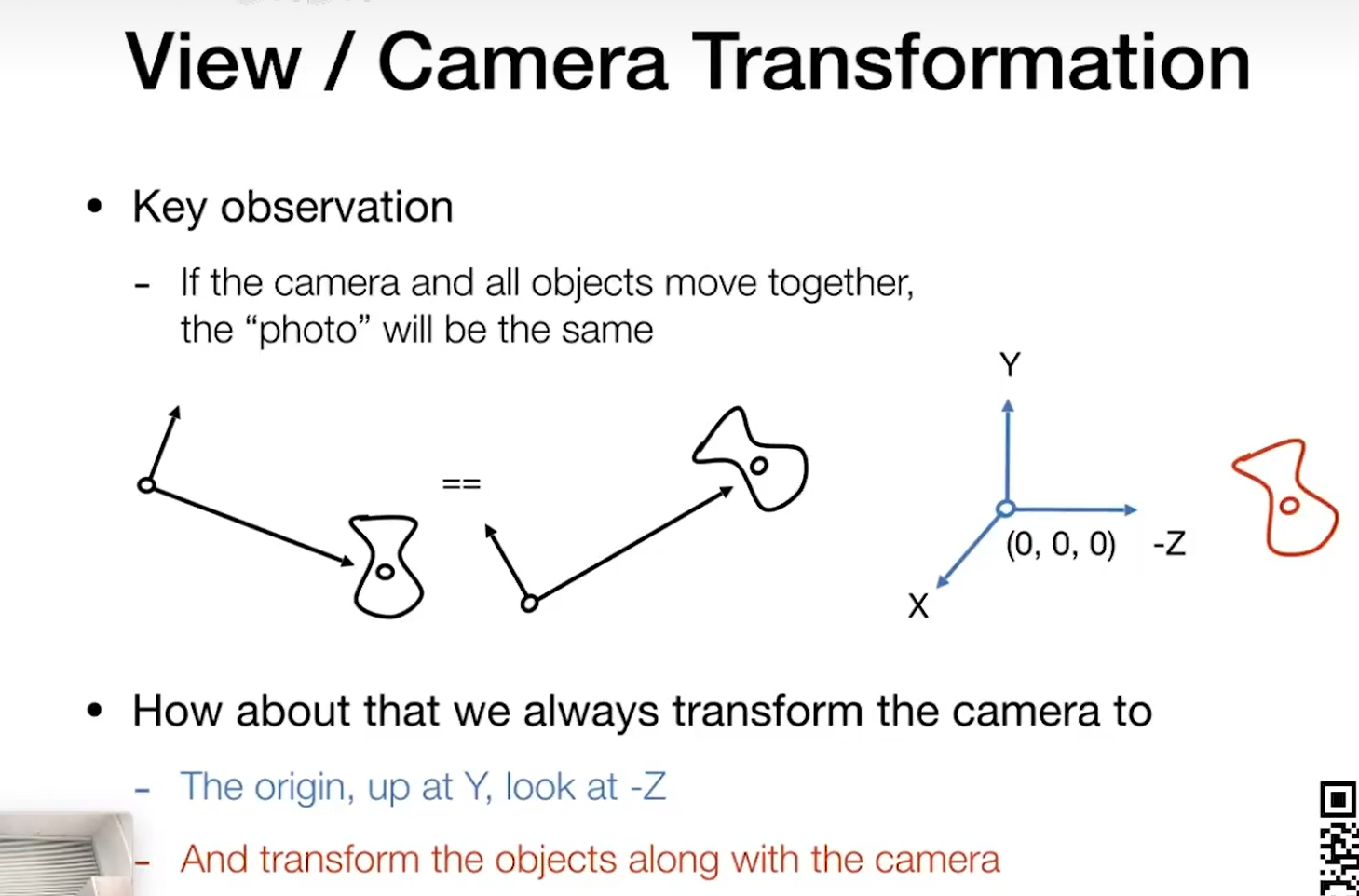
模型 视图 投影 视图变换 ~ 摆照相机(位置, 往那儿看look at direction, 向上方向up direction)

如何进行视图变换

相机固定不动,永远放在原点,往-z方向看,向上方向是y轴

如何将相机放到标准位置上呢?

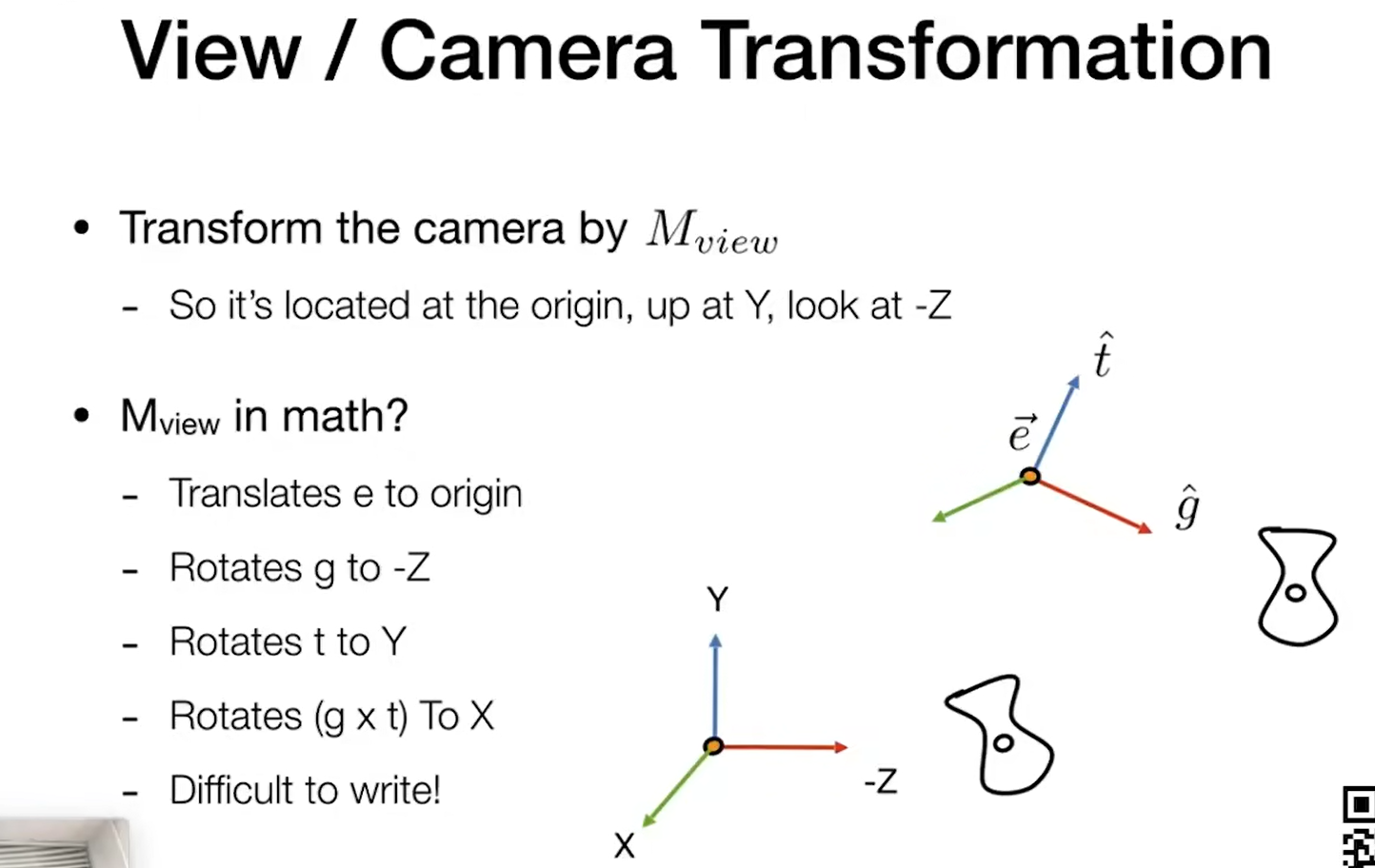
1. 先把e平移到0
2. 把观察的方向g旋转到-z,向上的方向t移动到y方向

原变换不好写,通过逆变换来写 旋转矩阵是正交矩阵,逆是转置

投影:

1. 正交投影
2. 透视投影(会带来一种近大远小的现象)

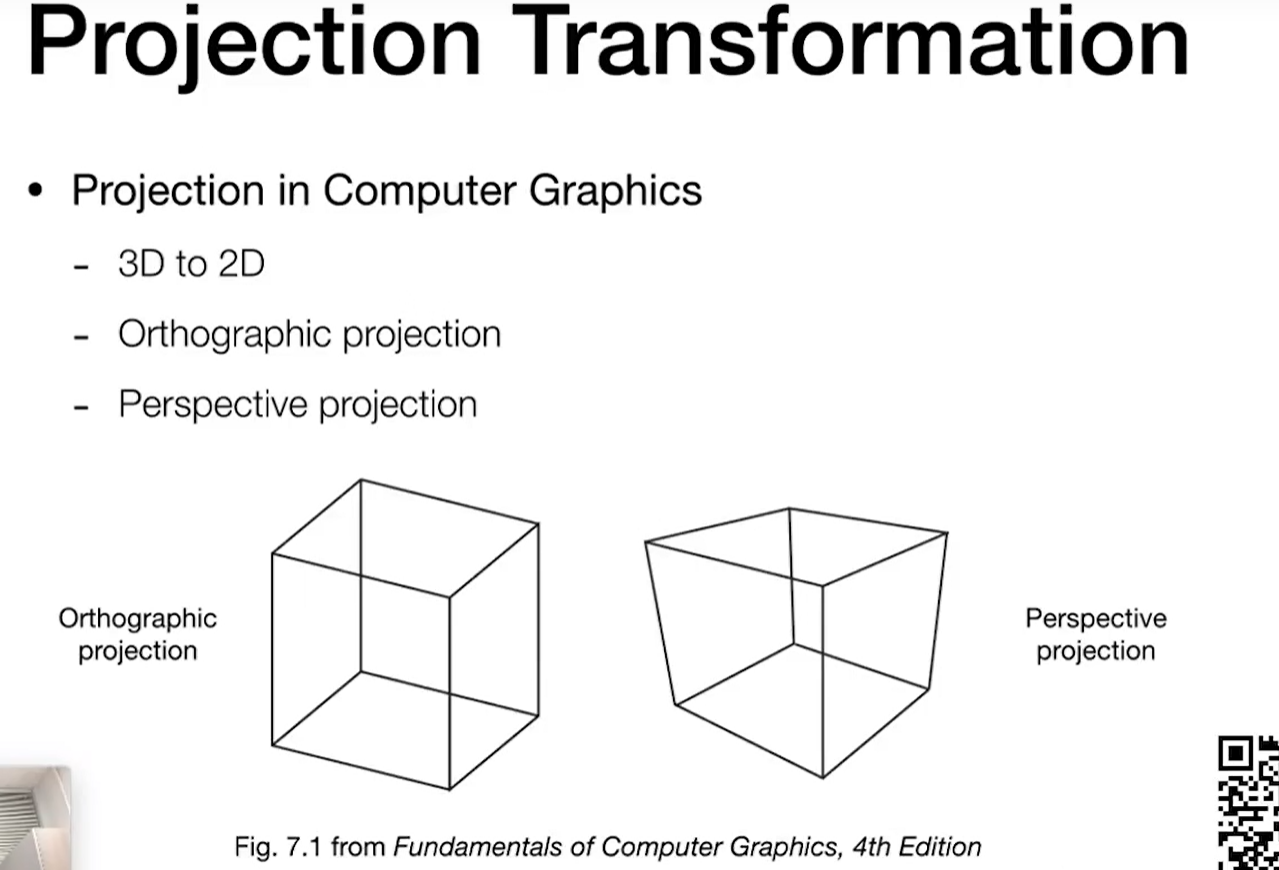
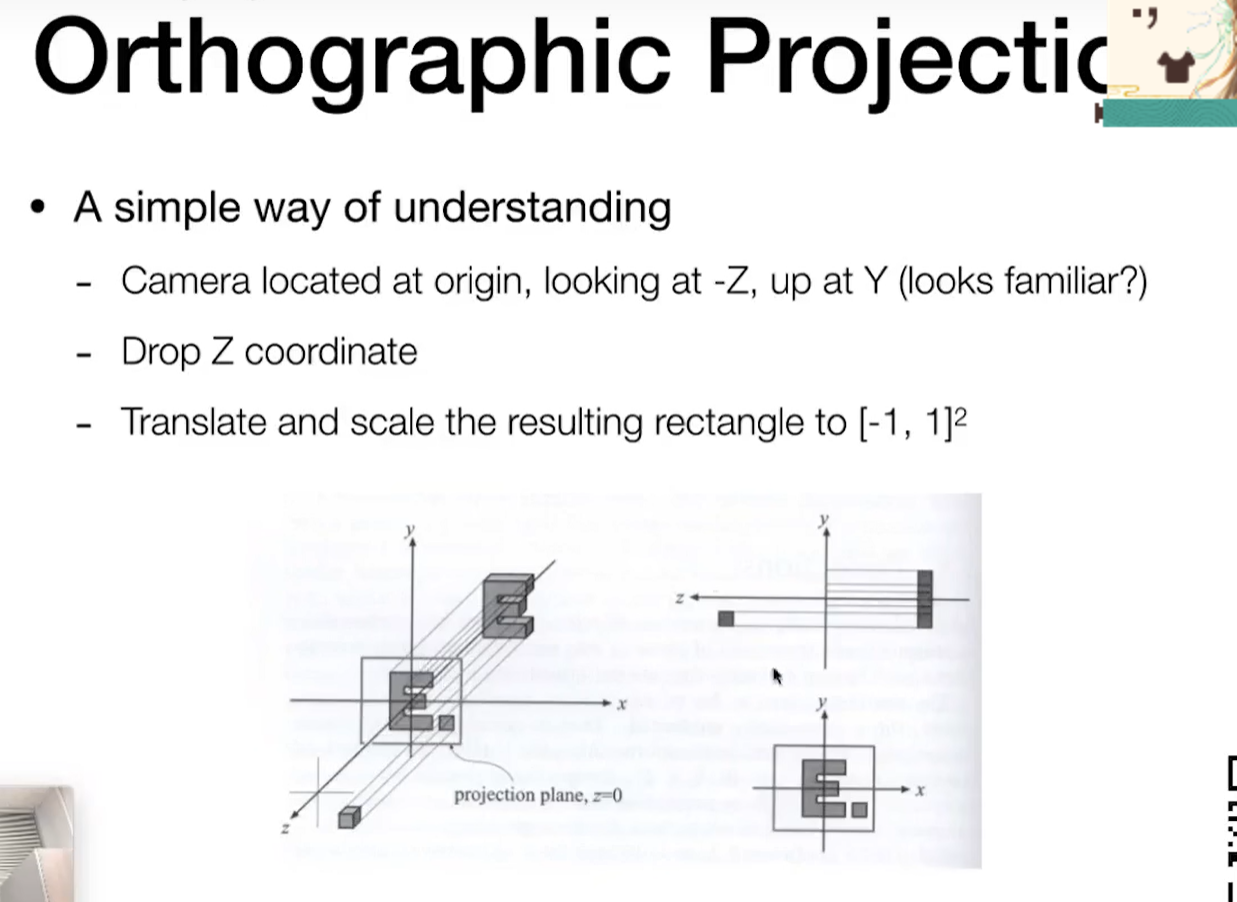
对于正交投影,假设相近放在无限远处

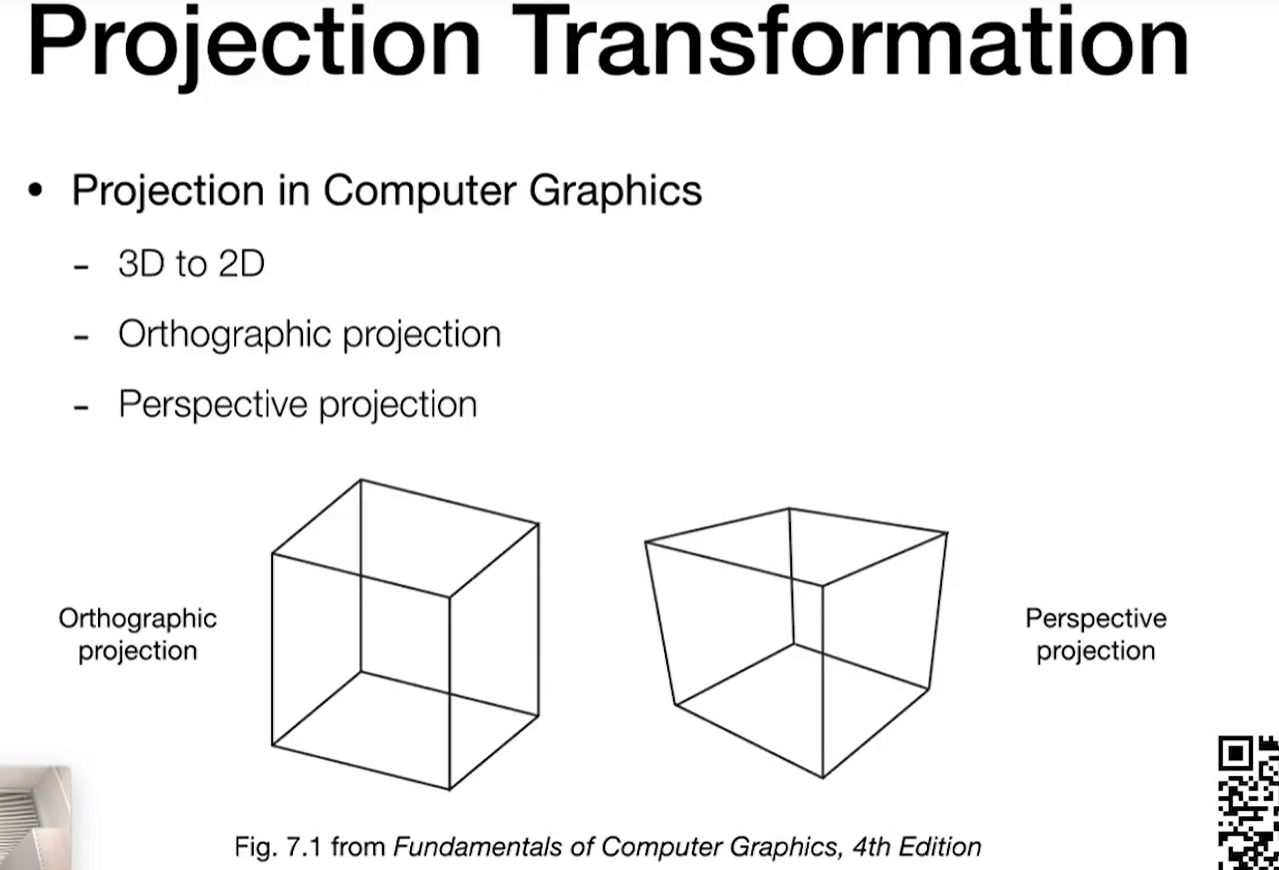
把对应的z给丢掉

但是这样如何区分物体的前和后呢?

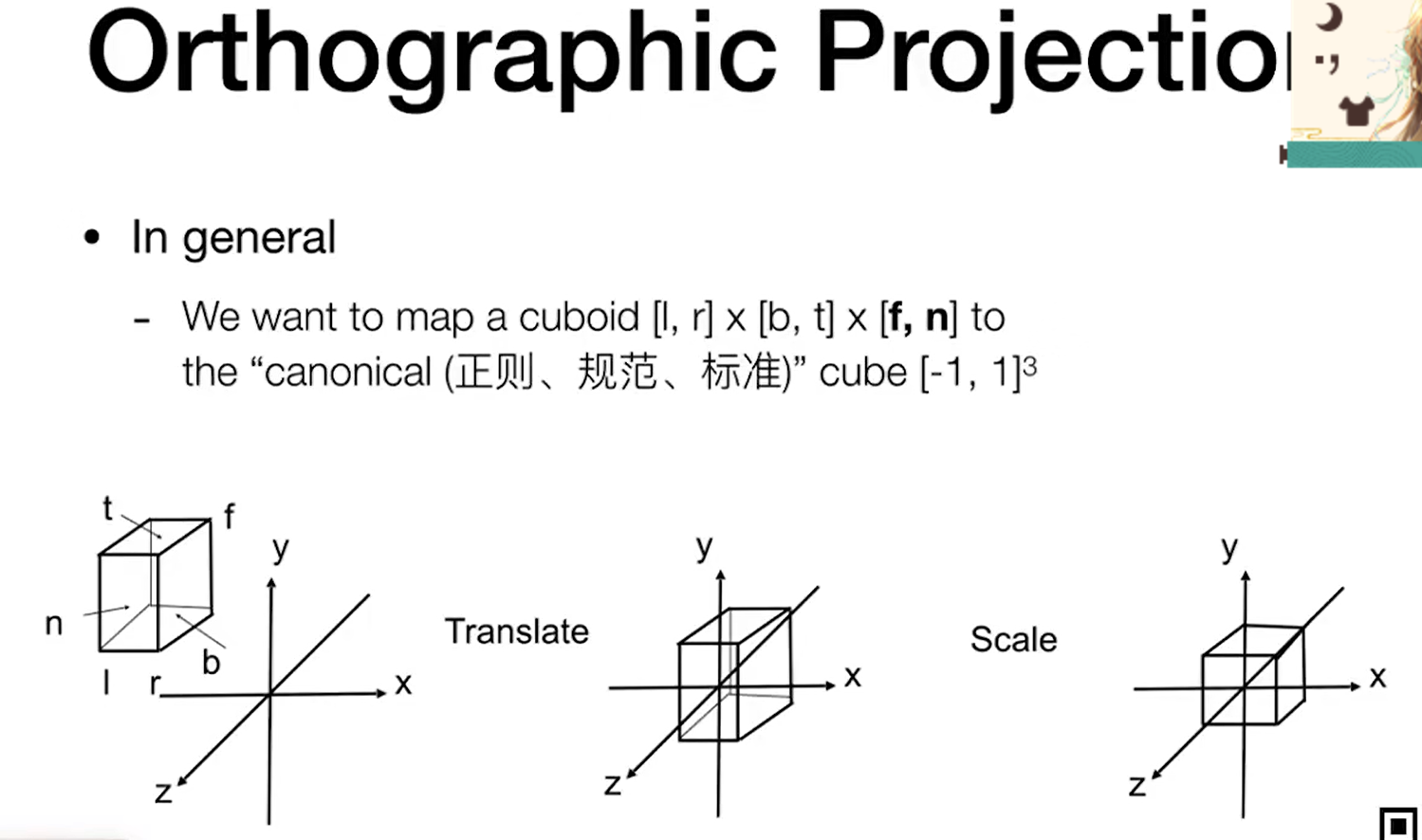
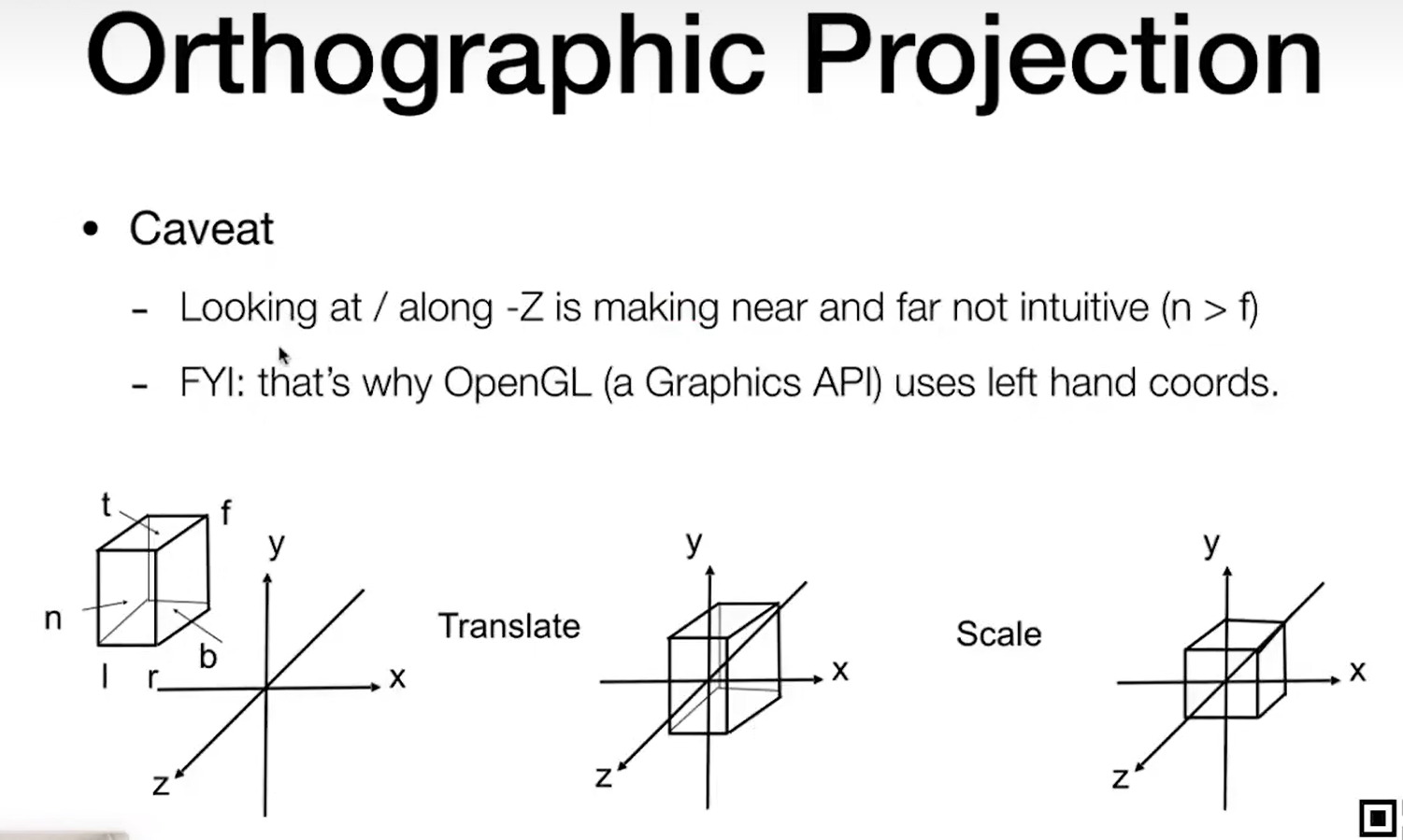
任意给一个长方体将其映射为中心为原点的立方体

上述变换的矩阵表示: 先做平移移动到原点上,然后再做缩放

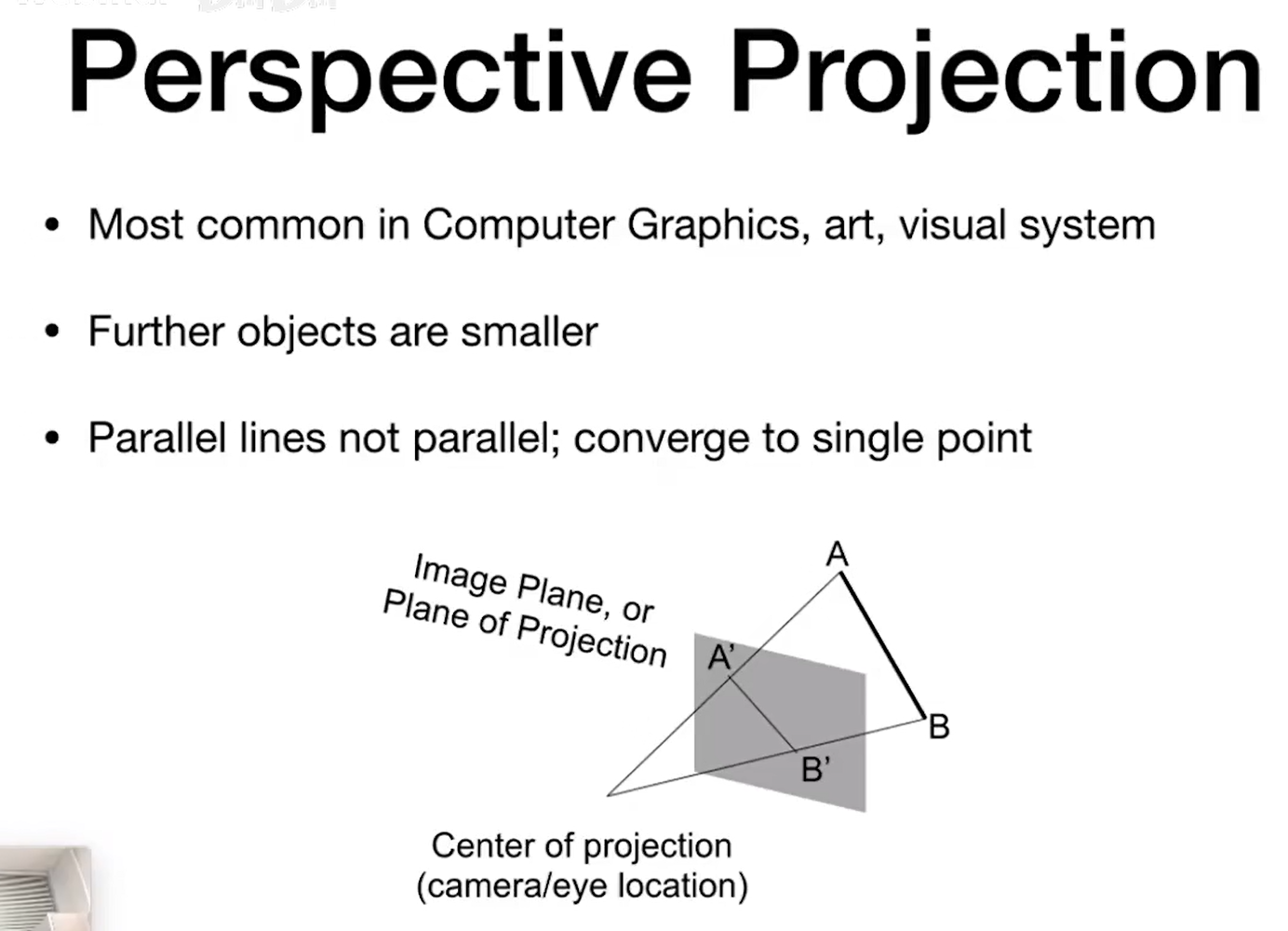
平行线不相交

在透视投影下,两个

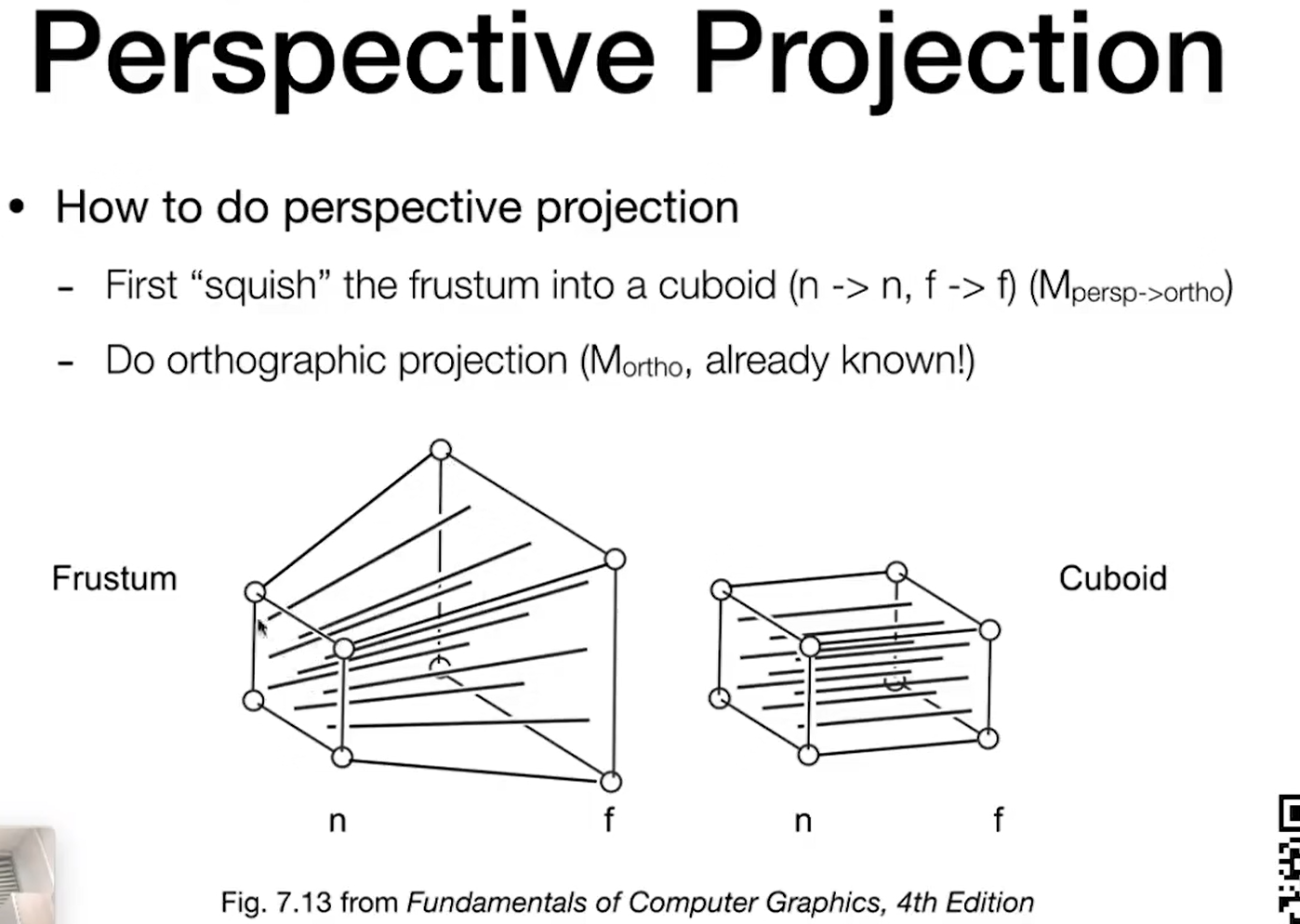
透视投影非常困难 近平面永远不变

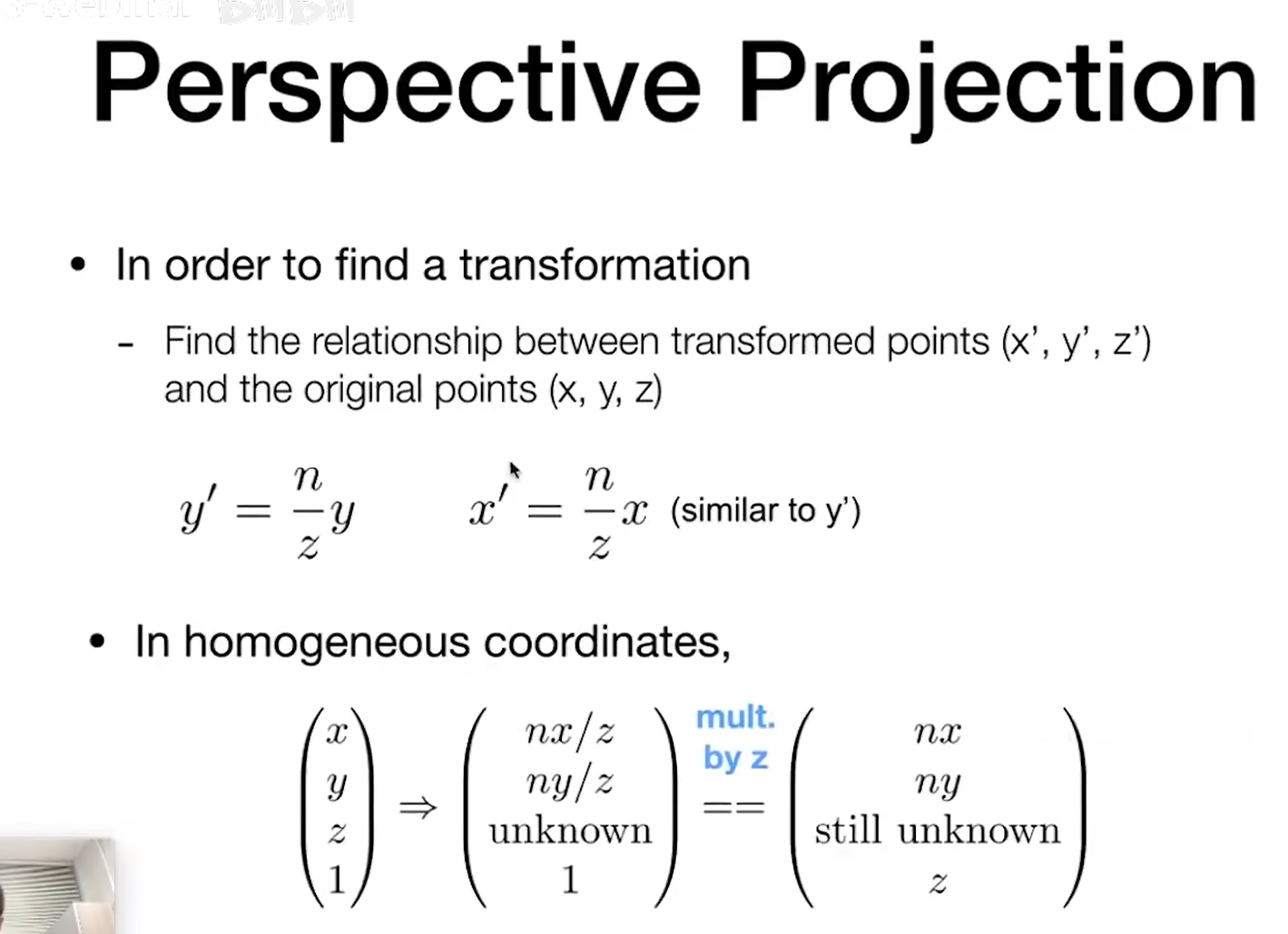
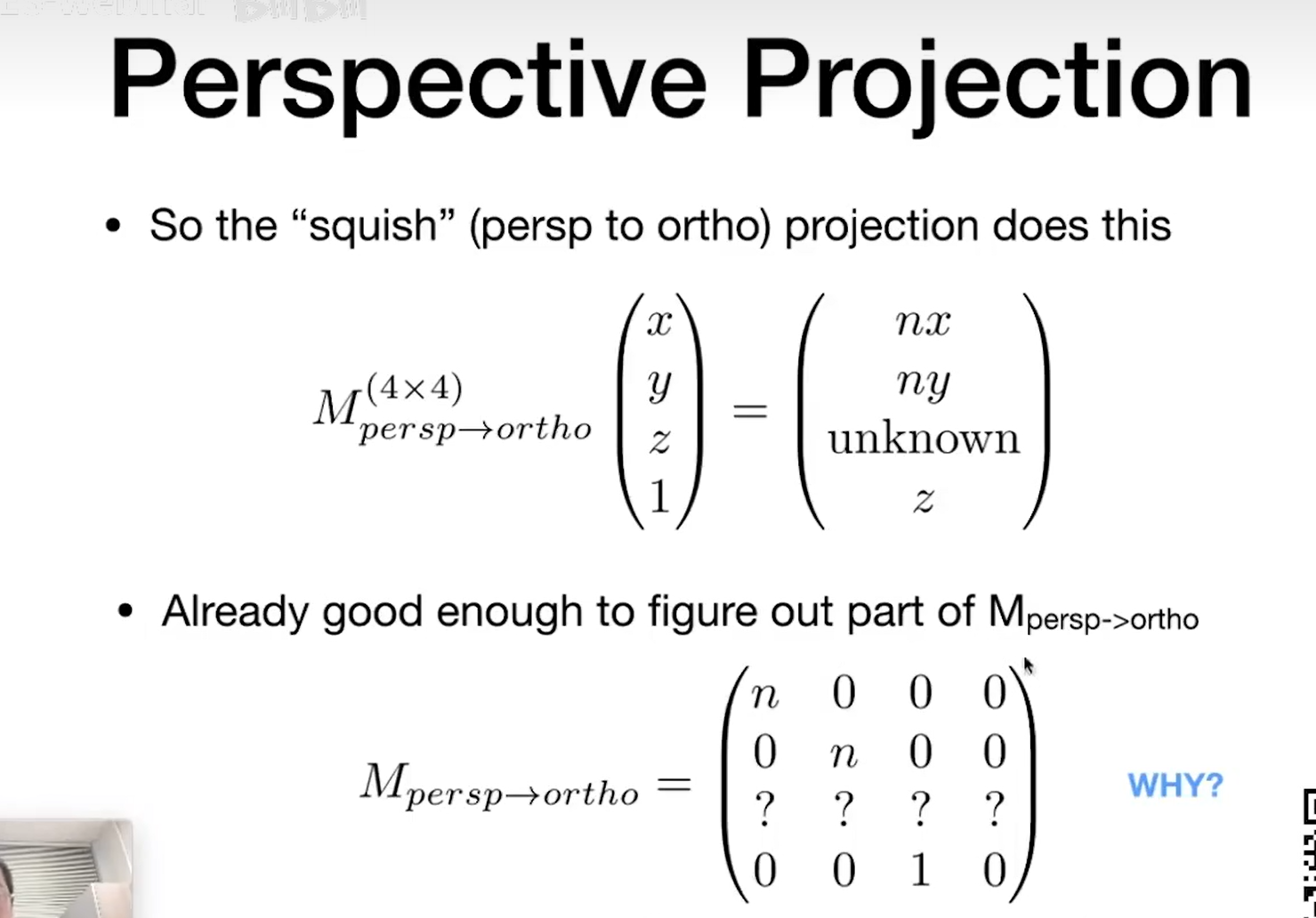
在近的平面和远的平面上z不会发生任何变化.

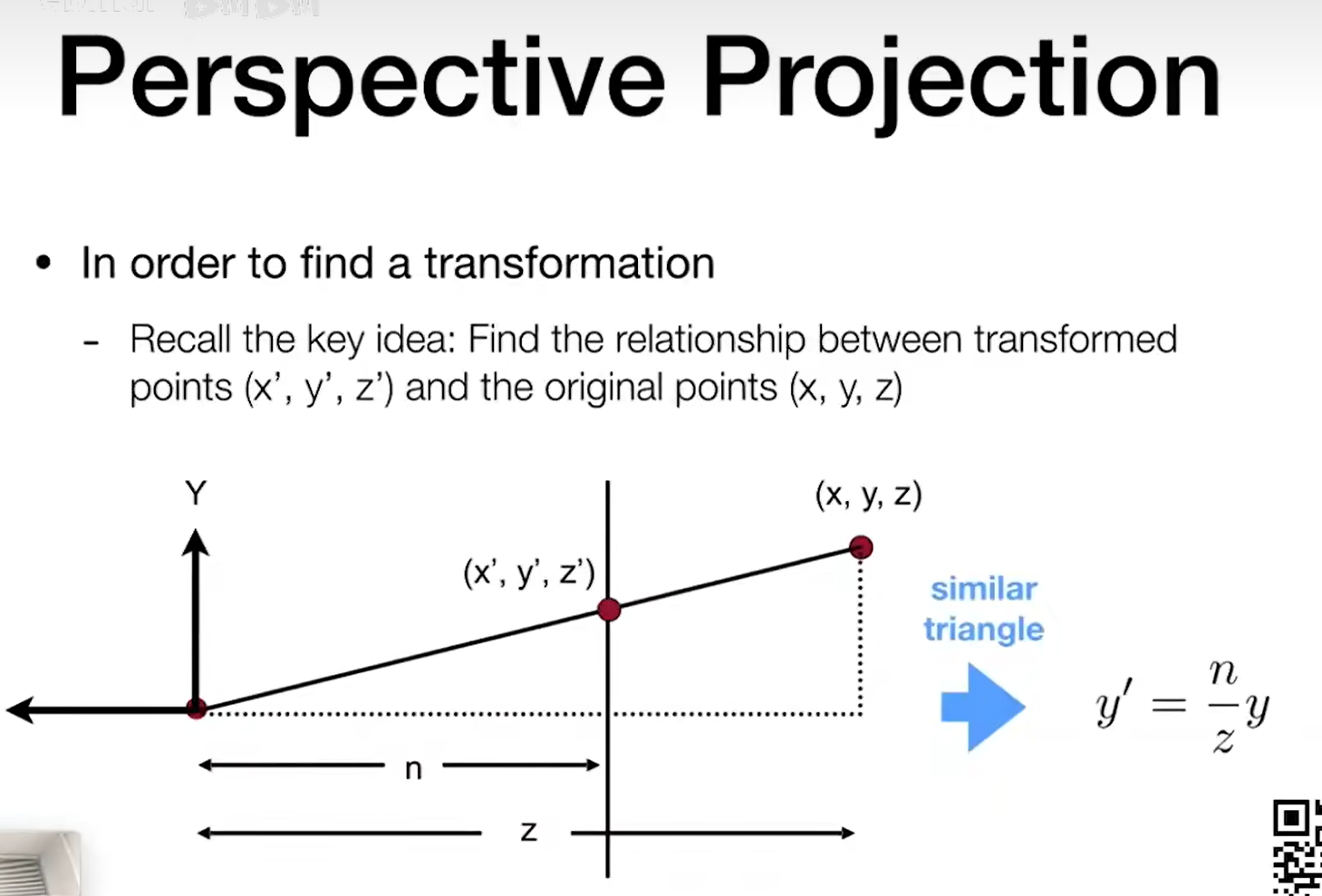
中间的点在经过挤压后z该如何变化?

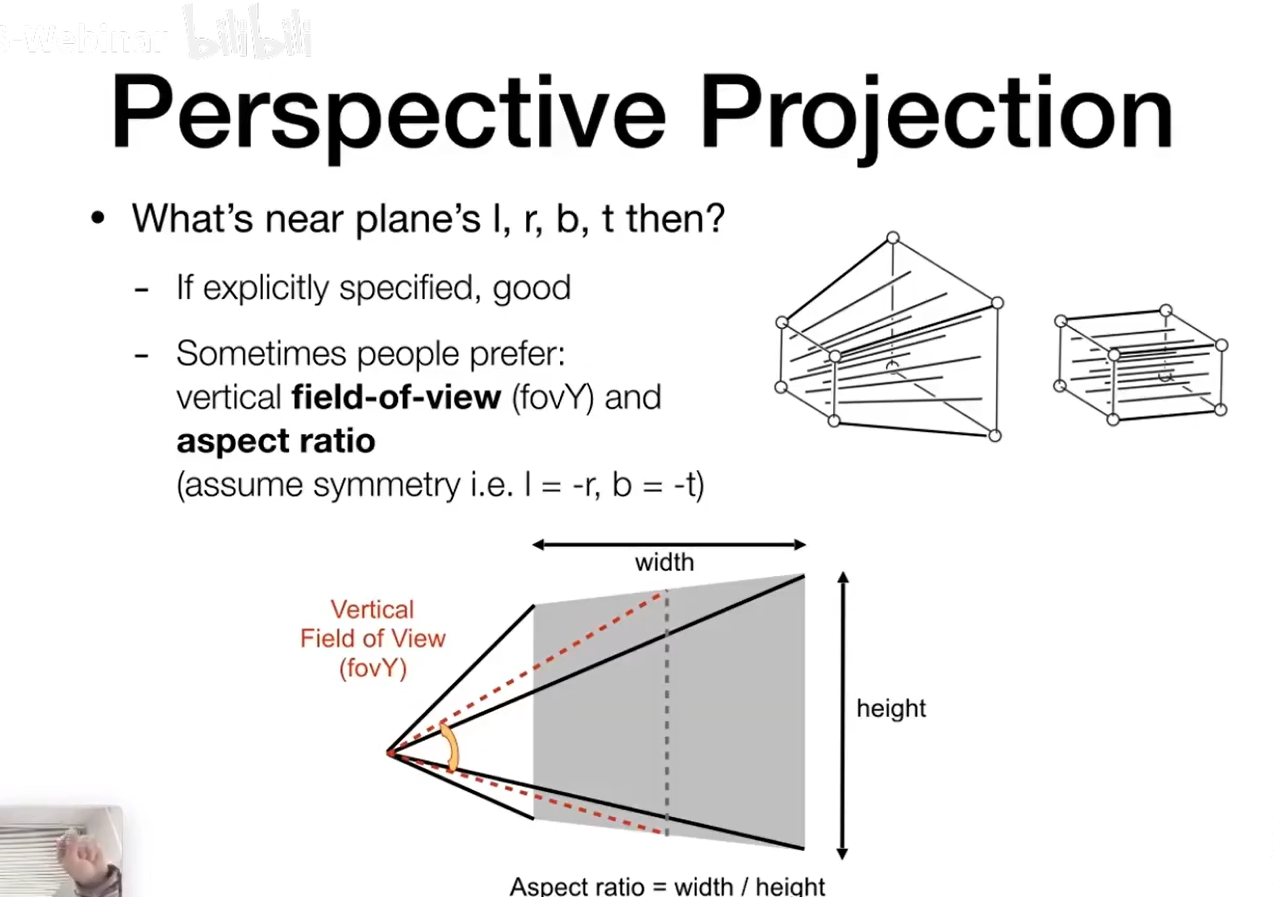
如何定义这样一个丝锥? 长宽比 视角

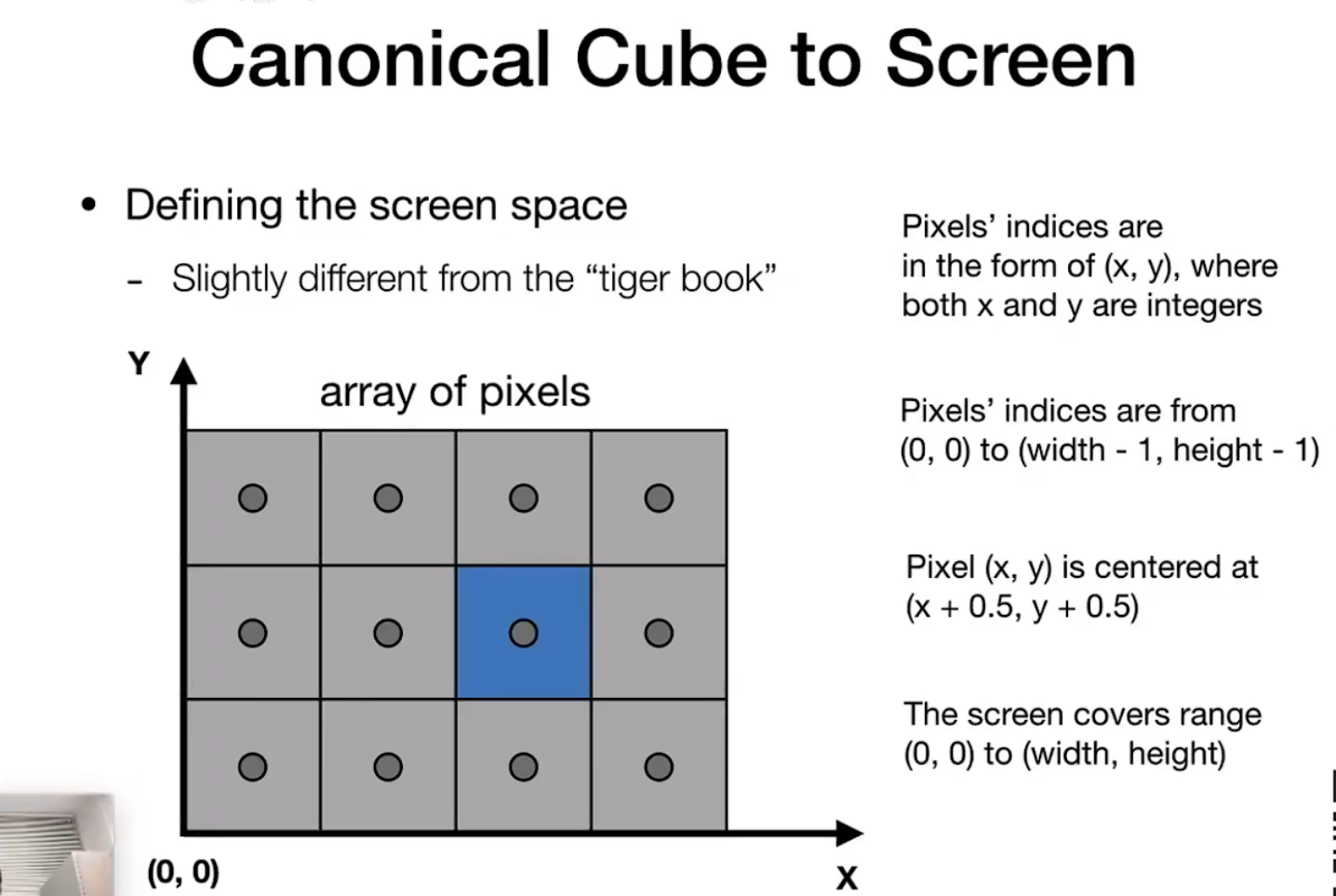
什么是屏幕?

什么是屏幕的空间?

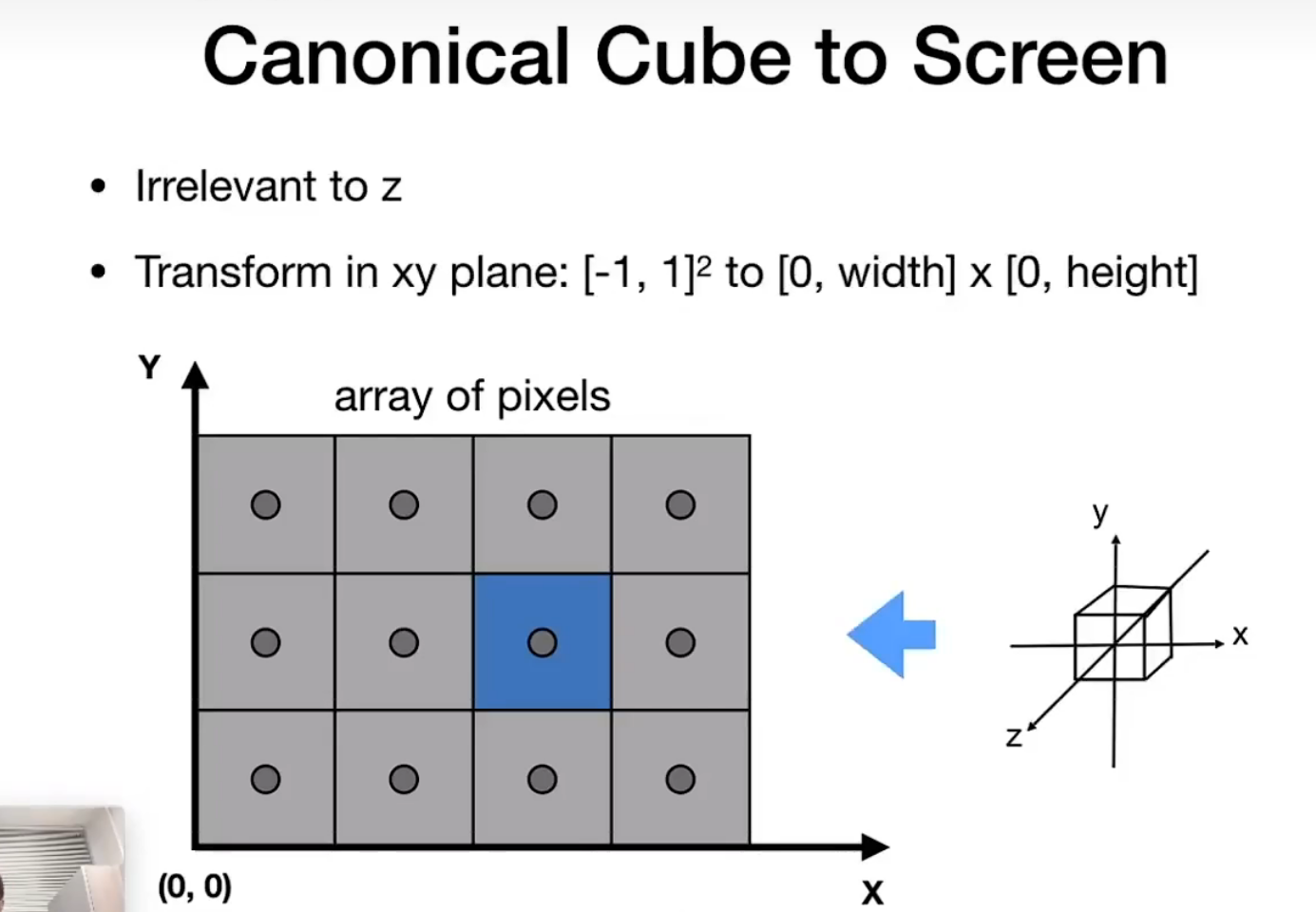
保留z方向不变

采样的方法 把一个函数给离散化 利用像素中心对屏幕空间进行采样

真实的像素的构成: dayer pattern

---