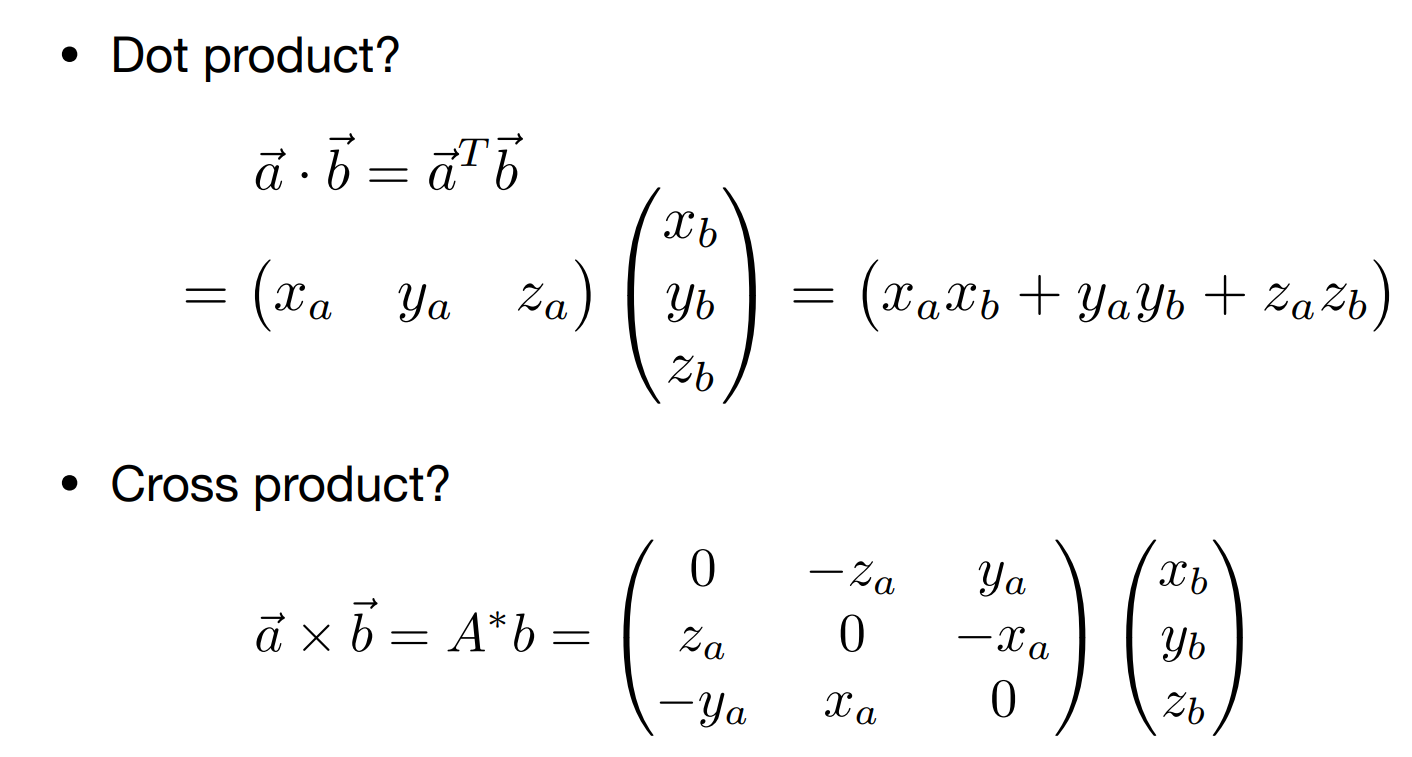Link Search Menu Expand Document
GXL-Groups
目录
  1. 向量与线性代数
    1. 向量Vector
      1. 1. 向量的表示
      2. 2. 向量长度与单位向量
      3. 3. 向量加法(四边形法则与三角形法则)
      4. 4. 笛卡尔坐标下向量的表示
      5. 5. 向量点乘dot product
      6. 6. 向量叉乘Cross product
      7. 7. 正交基坐标系
    2. 矩阵Matrices

向量与线性代数

阅读材料:参考书第2章(Miscellaneous Math), 第5章(Linear Algebra)

图形学依赖于:

  • 基本的数学: 线性代数,微积分,统计学
  • 基本的物理: 光学, 机械
  • 其它: 信号处理, 数值分析
  • 一定的美学

这一门课程大部分依赖于线性代数,包括向量(点乘,叉乘,…),矩阵.

一些基本的观点, 一个点可以表示为向量;翻转旋转物体等操作可以表现为矩阵-向量的乘积运算

向量Vector

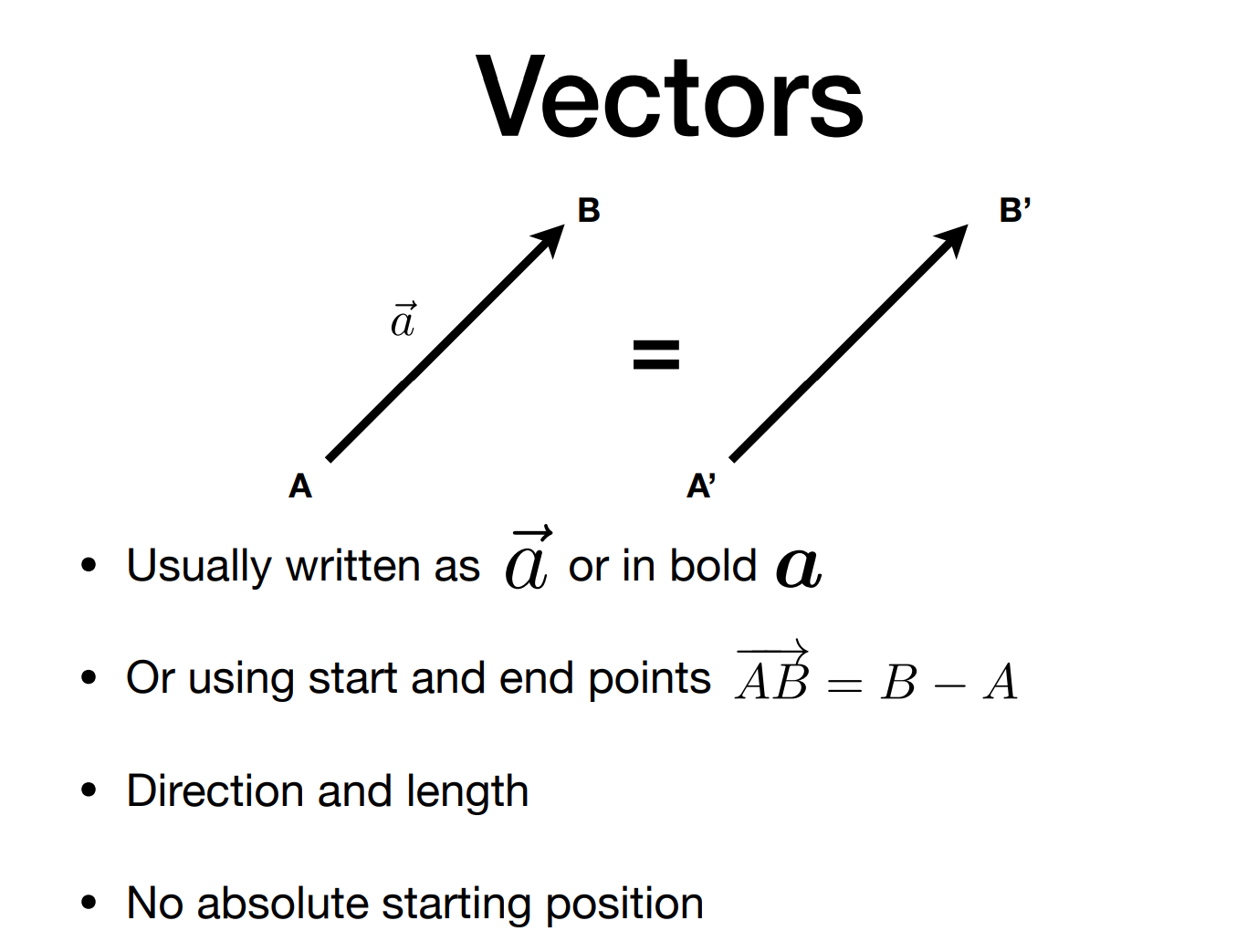
1. 向量的表示

  • 字母上面加箭头 $\vec{a}$ 或者黑体加粗 $\boldsymbol{a}$
  • 使用起点和终点:$\vec{AB} = B - A$

2. 向量长度与单位向量

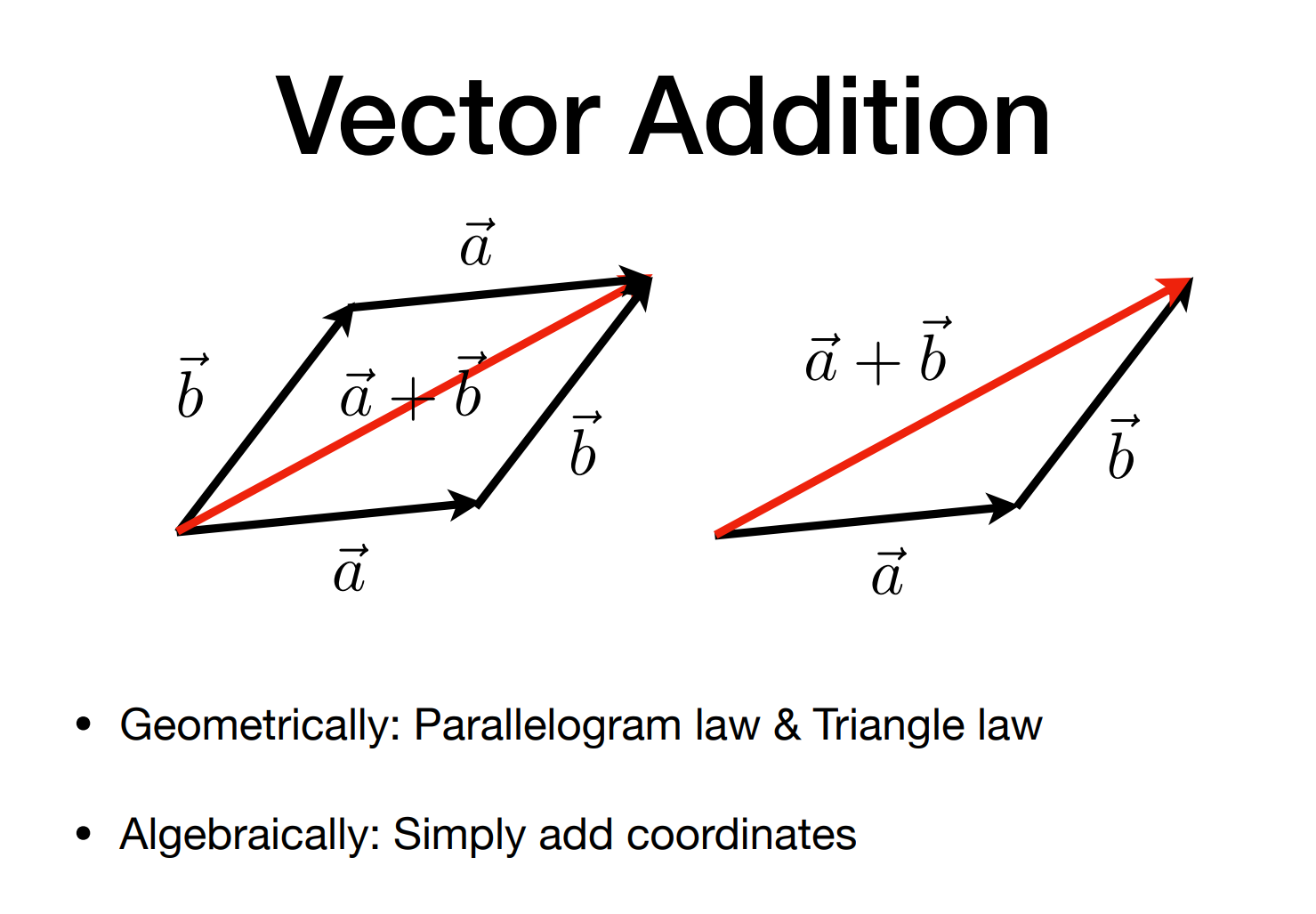
3. 向量加法(四边形法则与三角形法则)

4. 笛卡尔坐标下向量的表示

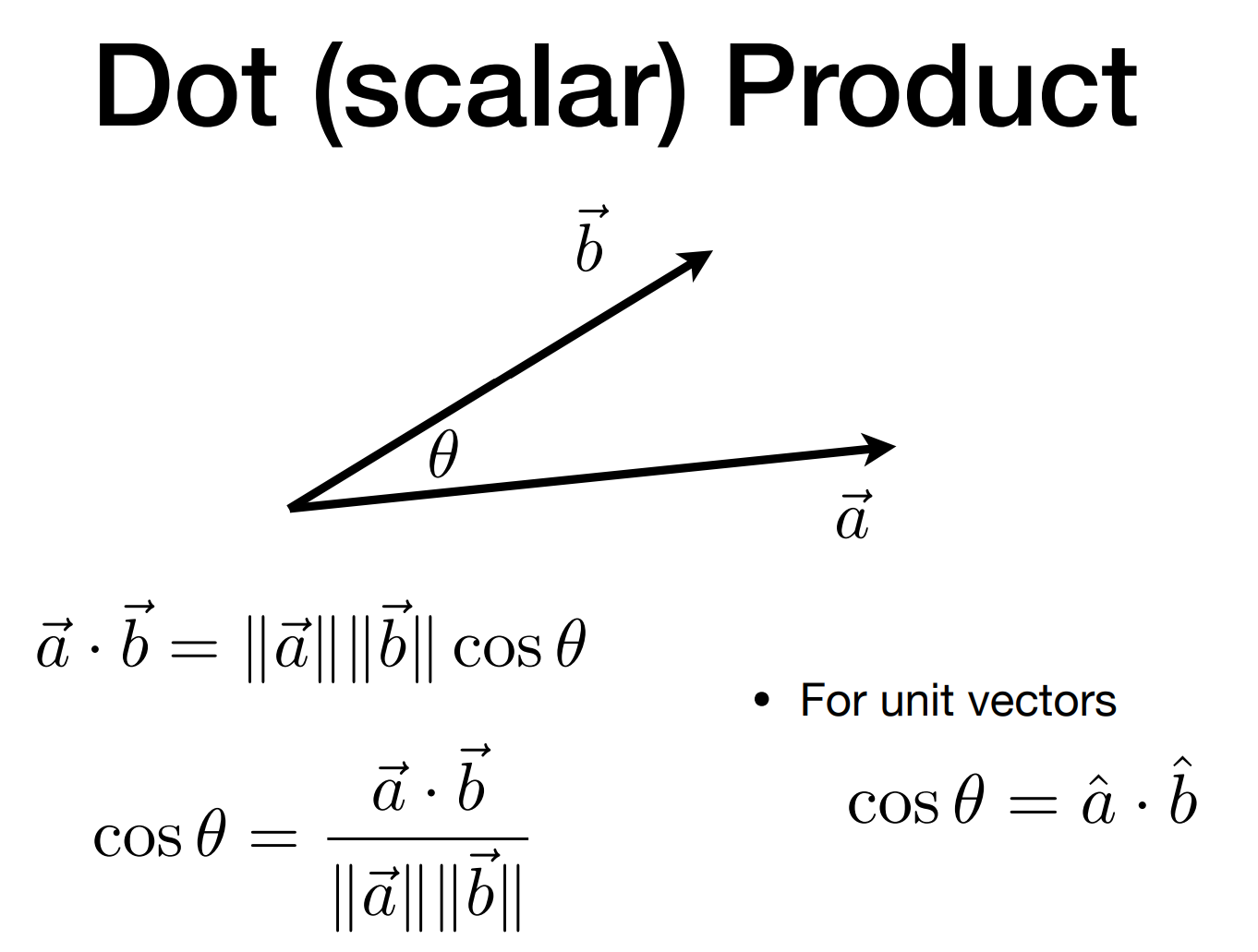
5. 向量点乘dot product

\[\vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta \\ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|}\]
  • 对于单位向量 $\cos \theta=\hat{a} \cdot \hat{b}$

  • 性质 \(\begin{array}{l} \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} \\ \vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} \\ (k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b}) \end{array}\)

  • 笛卡尔坐标系下点乘的表示(逐个分量做乘法,然后相加)

\[\vec{a} \cdot \vec{b}=\left(\begin{array}{l} x_{a} \\ y_{a} \end{array}\right) \cdot\left(\begin{array}{l} x_{b} \\ y_{b} \end{array}\right)=x_{a} x_{b}+y_{a} y_{b}\newline \vec{a} \cdot \vec{b}=\left(\begin{array}{c} x_{a} \\ y_{a} \\ z_{a} \end{array}\right) \cdot\left(\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right)=x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}\]

  • 点乘的投影:

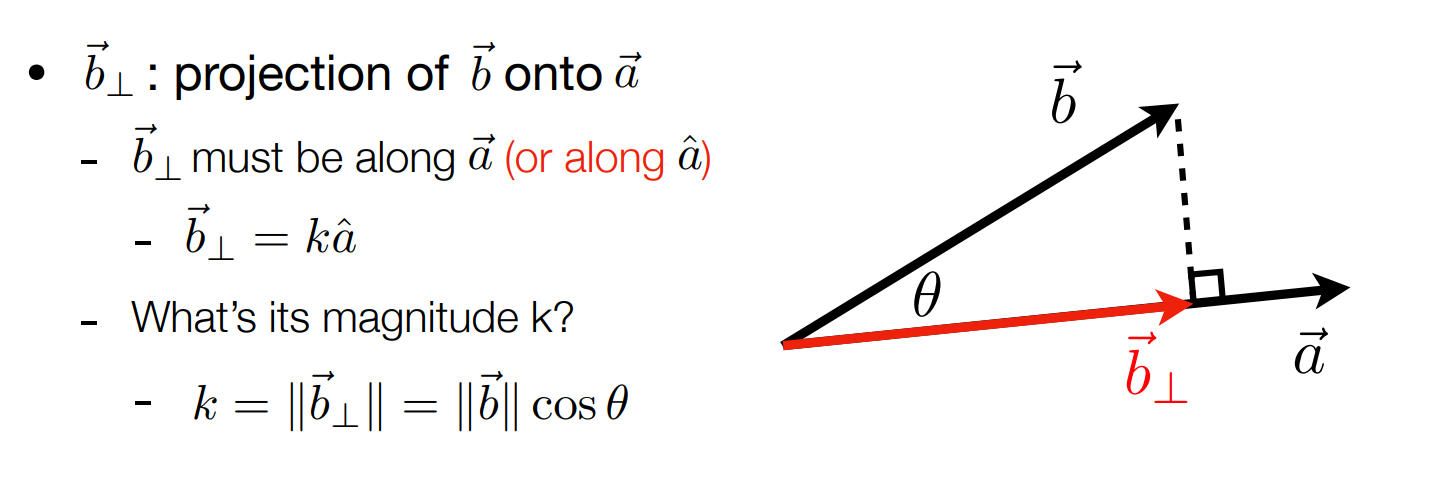
  • 点乘的应用:

    • 度量两个向量方向是否接近(如果两个都是单位向量,点乘为1则方向十分接近,为0则是相互垂直,为-1,则方向相反)
    • 分解向量
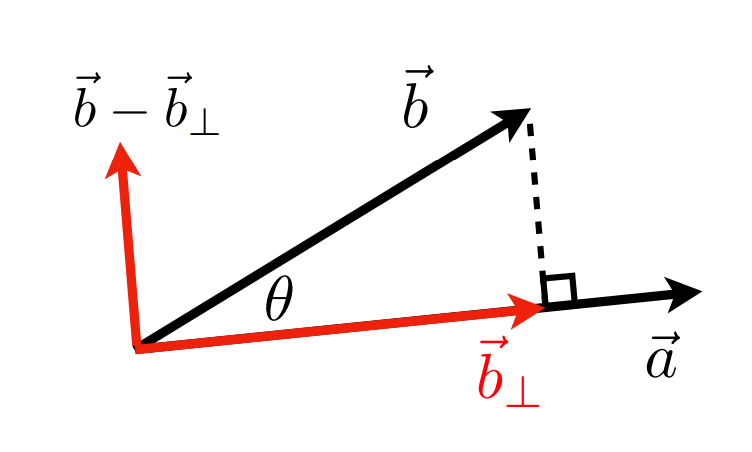
    • 判断方向是向前还是向后

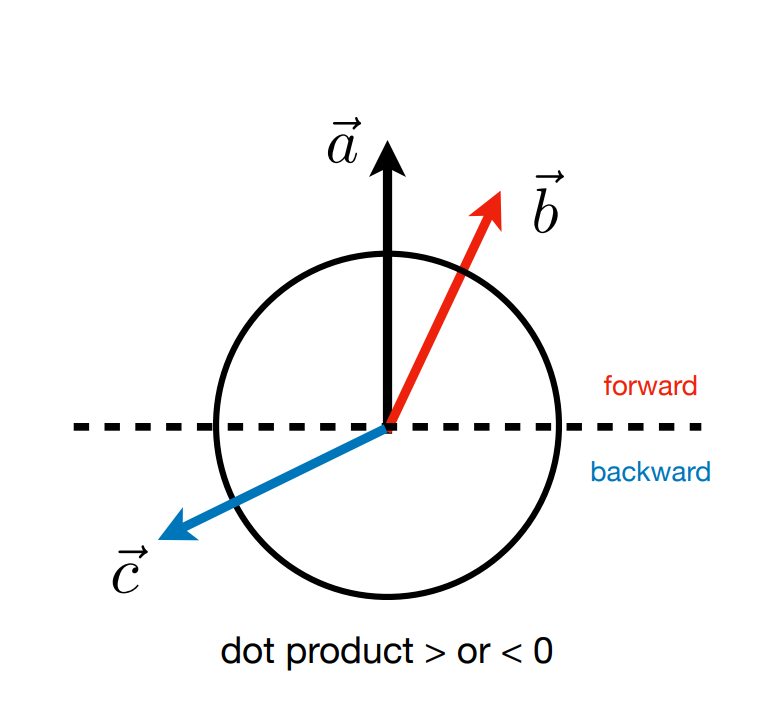
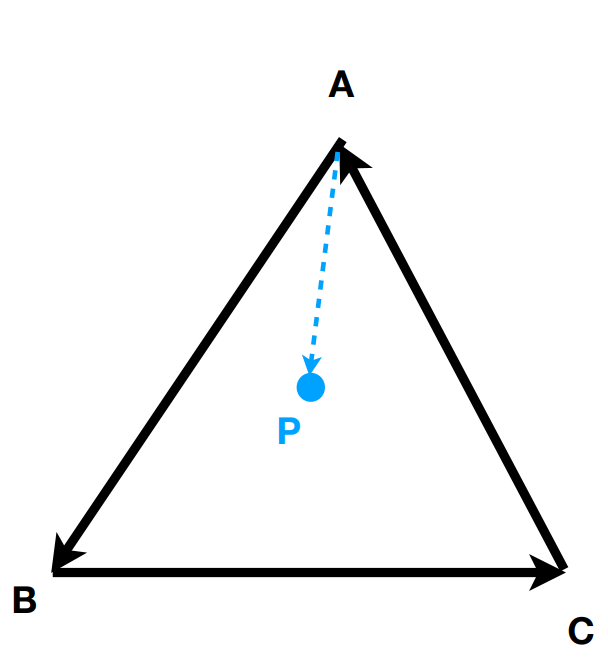
6. 向量叉乘Cross product

向量叉乘的结果垂直于原来的两个向量;通过右手定则确定叉乘的结果的方向;在构造坐标系的时候非常有用

  • 性质: \(\begin{array}{lc} \vec{x} \times \vec{y}=+\vec{z} & \vec{a} \times \vec{b}=-\vec{b} \times \vec{a} \\ \vec{y} \times \vec{x}=-\vec{z} & \vec{a} \times \vec{a}=\overrightarrow{0} \\ \vec{y} \times \vec{z}=+\vec{x} & \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} \\ \vec{z} \times \vec{y}=-\vec{x} & \vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b}) \\ \vec{z} \times \vec{x}=+\vec{y} & \\ \vec{x} \times \vec{z}=-\vec{y} & \end{array}\)

  • 笛卡尔坐标系下表示 \(\vec{a} \times \vec{b}=\left(\begin{array}{c} y_{a} z_{b}-y_{b} z_{a} \\ z_{a} x_{b}-x_{a} z_{b} \\ x_{a} y_{b}-y_{a} x_{b} \end{array}\right) \newline \vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc}0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0\end{array}\right)\left(\begin{array}{l}x_{b} \\ y_{b} \\ z_{b}\end{array}\right)\)

  • 几何意义

    • 判断左右方向

    • 判断点在图形外部还是内部

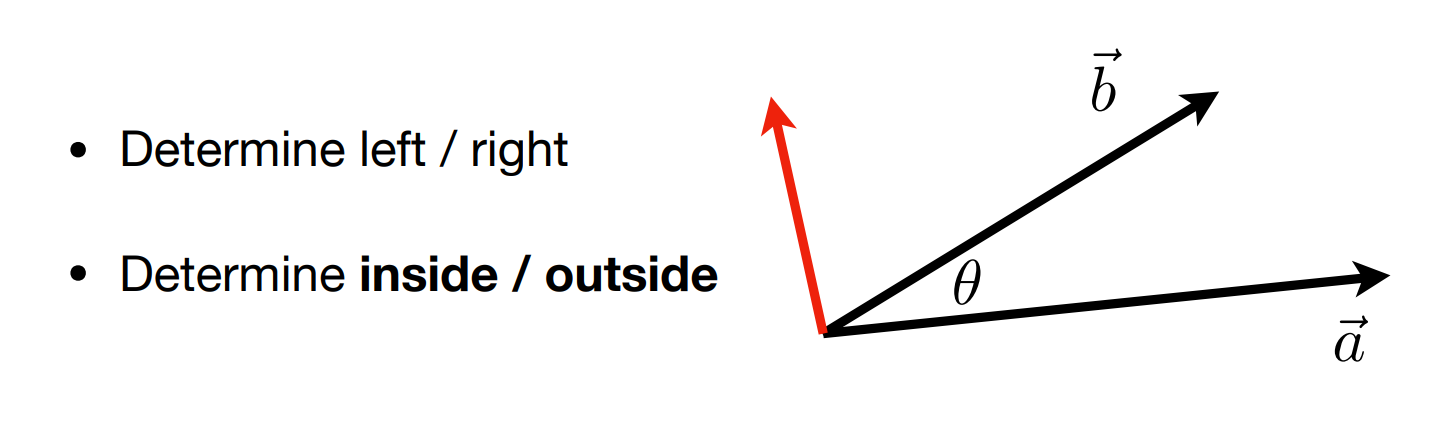
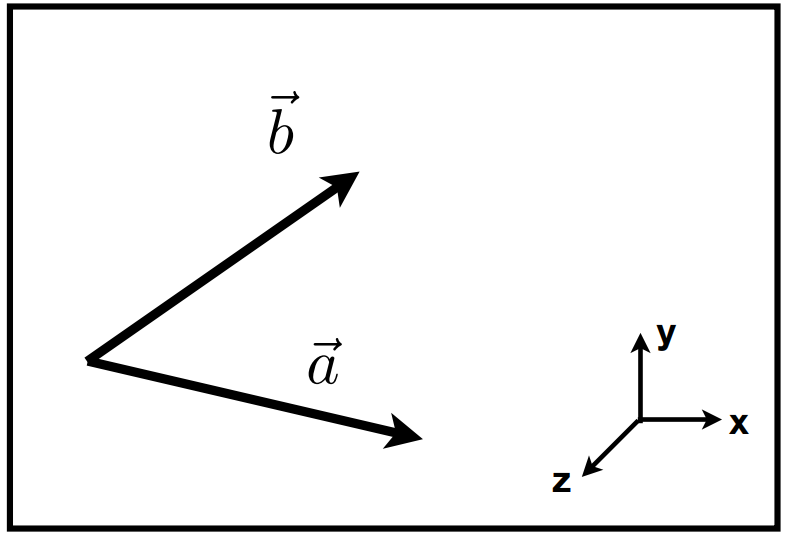
      比如下面的点p在三角形内部

7. 正交基坐标系

三维正交坐标系: \(\begin{array}{l} \|\vec{u}\|=\|\vec{v}\|=\|\vec{w}\|=1\\ \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0\\ \vec{w}=\vec{u} \times \vec{v} \text { (right-handed) }\\ \vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w}\\ \text { (projection) } \end{array}\)

矩阵Matrices

  1. 什么是矩阵?

  1. 矩阵乘法

  1. 矩阵乘法的性质
  • 不满足对称性
  • 结合律和分配律都满足
  1. 矩阵向量相乘

  1. 矩阵转置

  1. 单位矩阵和逆

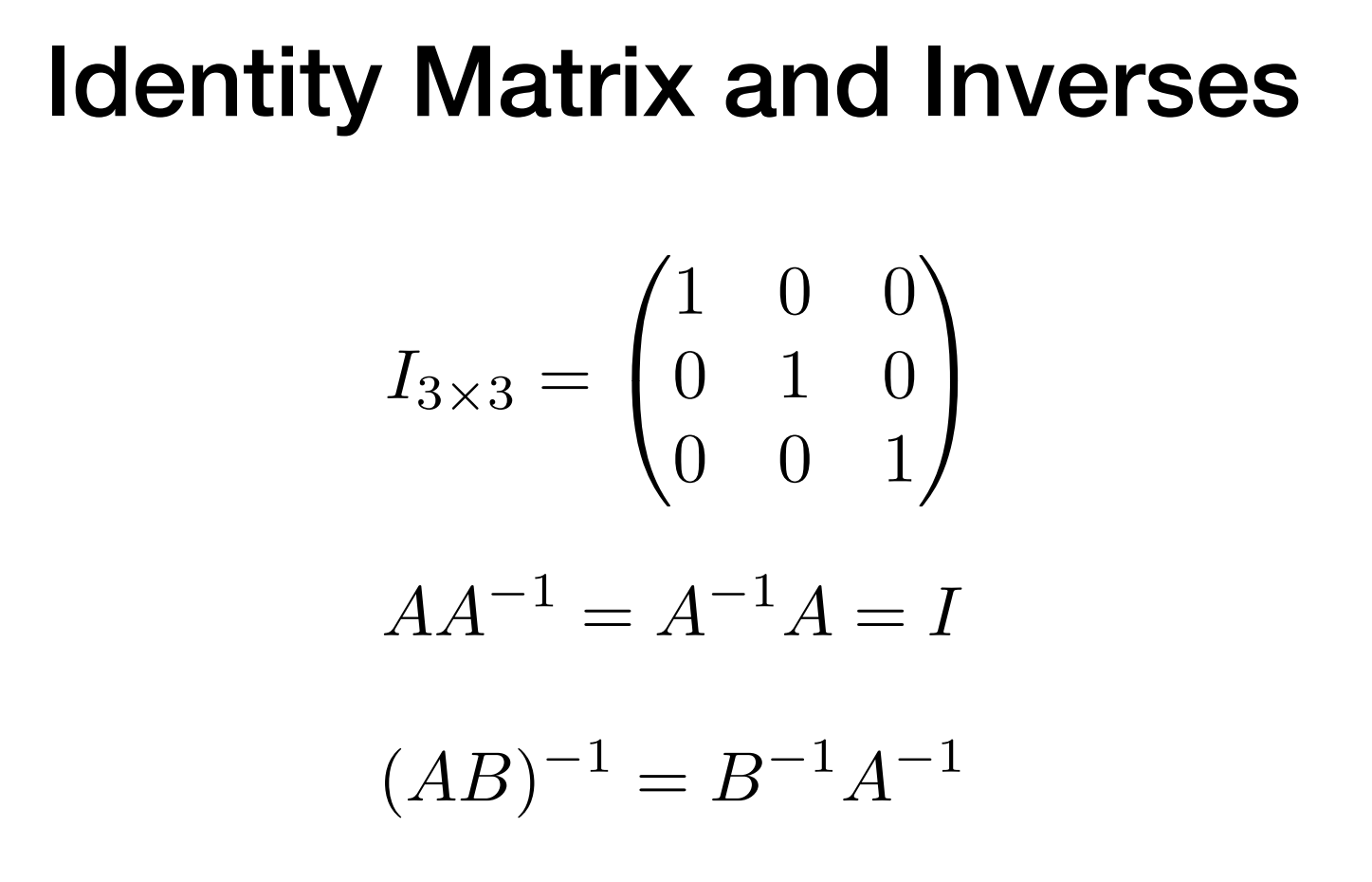
  1. 向量乘法的矩阵表达